Séminaire Itinérant de Catégories

Lieu: Labo de math de l’Université du Littoral à Calais (plan d’accès), salle B.014, et par visioconférence.

Organisation: Isar Stubbe et Andrée Ehresmann (avec l’aide indispensable de Isabelle Buchard, Gaëlle Compiègne et Jean-Yves Théry, et le soutien financier de la Fédération de Recherche Mathématique des Hauts-de-France)

Inscription: La participation au séminaire est gratuite, mais une inscription est nécessaire. L’inscription se fait par simple e-mail à Isar Stubbe (isar.stubbe[at]univ-littoral.fr, remplacer [at] par @). Merci d’indiquer s’il s’agit d’une participation sur place ou par visioconférence. Le repas de midi et les pauses café seront offerts aux participants sur place; le lien de la visioconférence sera envoyé aux participants à distance.

Attention: Pour la participation sur place, il est obligé d’avoir le EU Digital COVID Certificate (ou “pass sanitaire” pour les Français): son QR code sera scanné à votre arrivée au labo! Par ailleurs, il est conseillé de consulter ces pages pour organiser votre voyage si vous traversez une frontière; notez que dans ce cas vous devez vous munir d’un engagement sur l’honneur dûment complété.

Programme:
10h30 – accueil avec café
11h00 – Dominique Bourn
11h50 – Aline Michel
12h40 – repas et café
14h00 – William Hautekiet
14h50 – Pierre-Alain Jacqmin
15h40 – café
16h10 – Zurab Janelidze
17h00 – fin

Titres et résumés (ordre alphabétique):
Dominique Bourn – Groupoïdes affines
Les groupoïdes abéliens ont été introduit au CT 1999 comme étant ceux pour lesquels, pour tout objet $x$, le groupe $Aut_x$ est abélien. Nous leur préférons aujourd’hui la dénomination affines, nous verrons dans un instant pourquoi. Dans les catégories de Mal’tsev et de Gumm, tous les groupoïdes internes sont affines.
Une autre façon de les introduire est de remarquer que tout groupoïde interne à une categorie $\mathbb{E}$:

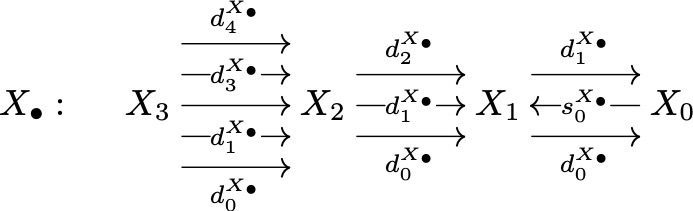
détermine sur l’objet $(d_0,d_1):X_1\to X_0\times X_0$ de la catégorie slice $\mathbb{E}/X_0\times X_0$ une loi de Mal’tsev associative définie par $p(\phi,\chi,\psi)=\phi.\chi^{-1}.\psi$ pour tout triplet de flèches parallèles. Un groupoïde est affine si et seulement si cette operation est de plus commutative (et par conséquent autonome puisqu’elle est déjà associative). Ainsi un groupoïde est affine si et seulement si, dans la fibre protomodulaire (et donc mal’tsevienne) $Grd_{X_0}$, l’objet $X_{\bullet}$ est un objet affine. Ainsi toute relation d’équivalence est trivialement un groupoïde affine.
La sous-catégorie $AffGrd_{X_0}\mathbb{E}\subset Grd_{X_0}\mathbb{E}$ est donc naturellement de Mal’tsev et, selon un schéma très général, quand $\mathbb{E}$ est exacte, elle permet la création des sommes de Baer des groupoïdes affines connexes ayant même direction dans la fibre.
Lorsque ces groupoïdes sont asphériques, i.e. lorsque, de plus, $X_0$ est à support global, on peut définir un invariant beaucoup plus fort puisque le groupoïde $X_{\bullet}$ devient faiblement équivalent à n’importe quel de ses groupes $Aut_x$, produisant un autre type de somme de Baer. De là, nous monterons également que, dans le cadre exact, lorsque $f_{\bullet}: X_{\bullet}\to Y_{\bullet}$ est une equivalence faible, $X_{\bullet}$ est affine si et seulement si $Y_{\bullet}$ l’est. Par conséquent lorsque $Y_{\bullet}$ est affine, c’est une relation d’équivalence si et seulement si $X_{\bullet}$ l’est.

William Hautekiet – Un théorème de comonadicité pour comodules partiels
Un module partiel à gauche sur une algèbre de Hopf $H$ est un espace vectoriel $M$ muni d’une application linéaire unitale $\rho : H \otimes M \to M$ qui satisfait une version affaiblie de l’associativité, appelée l’associativité partielle. Dans [1], il est montré que la catégorie des modules partiels à gauche sur $H$ est isomorphe à la catégorie des modules à gauche sur une autre algèbre $H_{par}$, qui porte la structure d’un algèbroïde de Hopf.
Cette situation est dualisée dans [2], ce qui donne les comodules partiels (à droite), c’est-à-dire espaces vectoriels munis d’une coaction co-unitale $M \to M \otimes H$ qui satisfait la coassociativité partielle. Par contre, il n’existe en général pas de cogèbre $C$ pour laquelle la catégorie des comodules partiels sur $H$ est équivalente à la catégorie de comodules (usuels) sur $C$.
On montre que la catégorie des comodules partiels sur $H$ est comonadique sur $\mathsf{Vect}_k$, alors elle est équivalente à la catégorie d’Eilenberg-Moore d’une comonade $\mathbb{C}$. Dans cet exposé, la construction de cette comonade est présentée, et sa structure est explorée.
[1] Marcelo Muniz S. Alves, Eliezer Batista, Joost Vercruysse, Partial representations of Hopf algebras, Journal of Algebra, Volume 426, 2015, Pages 137-187, ISSN 0021-8693, https://doi.org/10.1016/j.jalgebra.2014.12.011.
[2] Marcelo Muniz S. Alves, Eliezer Batista, Felipe Castro, Glauber Quadros, Joost Vercruysse, Partial corepresentations of Hopf algebras, Journal of Algebra, Volume 577, 2021, Pages 74-135, ISSN 0021-8693, https://doi.org/10.1016/j.jalgebra.2021.03.001.

Pierre-Alain Jacqmin – Propriétés d’exactitude et leur caractérisation variétale
Étant donnée une propriété d’exactitude catégorique, comment caractériser les catégories algébriques (variétés) la satisfaisant? La littérature regorge d’exemples de telles caractérisations, souvent au moyen d’une condition de Mal’tsev. Pour répondre à cette question, nous allons d’abord définir de manière formelle une large classe de propriétés d’exactitude contenant notamment la protomodularité, l’unitalité et la propriété d’être une catégorie de Mal’tsev. Cette définition formelle repose sur la notion d’esquisses au sens de C. Ehresmann. Ensuite, en utilisant des extensions de Kan à gauche, nous étendrons la théorie des opérations approximées au sens de D. Bourn et Z. Janelidze à ce contexte général. Ceci nous permettra de caractériser les catégories régulières finiment cocomplètes satisfaisant une telle propriété d’exactitude. Nous appliquerons ensuite cette caractérisation au cas variétal pour répondre à la question initialement posée.
Une partie de ces résultats est un travail en collaboration avec Zurab Janelidze.

Zurab Janelidze – Forms vs monoidal categories
By a “form” we mean a faithful amnestic functor. Such functors are of course a very old object of study. They arise naturally in categorical logic, categorical topology, as well as in the notion of a concrete category. In all of these topics, however, the emphasis is on the domain category of the functor. In the theory of forms, one regards the codomain of the functor as the main object of study, treating a form as an additional information that category is equipped with. This approach is very similar to the study of fibrations in topology and the original approach of Grothendieck in the theory of (categorical) fibrations. The fibres of a form are to be seen as abstractly specified posets of subobjects, quotient objects, or their combination. Functorial duality plays a significant role in the development of the theory: one is interested in axioms on a form that are invariant under switching to the dual form (functor). Forms have applications in the analysis of homomorphisms theorems for group-like structures in algebra, in the theory of semi-abelian categories, as well as in the theory of categorical closure operators. While we will mention some of these applications, the main purpose of this talk is to explain an analogy between forms seen as categories equipped with a “posetal structure” and monoidal categories. We will see, in particular, that these two structures provide two intermediate streams of structural hierarchy that exist between the notion of an abelian category and the notion of a general category.

Aline Michel – Théories de torsion et revêtements des groupes préordonnés
Un groupe préordonné est un groupe muni d’un préordre qui est compatible avec la loi d’addition du groupe. Dans cet exposé, on s’intéresse à la catégorie PreOrdGrp des groupes préordonnés et des morphismes de groupes préservant le préordre. Nous utilisons tout d’abord plusieurs résultats intéressants développés dans [1] par Clementino, Martins-Ferreira et Montoli afin de trouver une théorie de torsion dans PreOrdGrp. Celle-ci induit un réflecteur « semi-left-exact » de PreOrdGrp vers sa sous-catégorie ParOrdGrp des groupes partiellement ordonnés, qui lui-même donne naturellement lieu à un système de factorisation $(E,M)$ où $M$ est la classe des revêtements triviaux (au sens de la théorie catégorique de Galois). La seconde partie de l’exposé est ensuite consacrée à la description de la classe $M^*$ (c’est-à-dire la « localisation » de la classe $M$), qui fournit ainsi une caractérisation assez simple des revêtements (au sens de la théorie catégorique de Galois) dans le contexte des groupes préordonnés. Il est également possible de décrire la classe $E’$ (la « stabilisation » de $E$) et de prouver que la paire $(E’,M^*)$ est un système de factorisation « monotone-light ». Cette présentation se base sur un article écrit en collaboration avec Marino Gran [2]. Une généralisation aux $V$-groupes (pour $V$ un quantale adéquat) des résultats exposés sera aussi très brièvement abordée [3] (avec plus ou moins de détails, selon le temps restant).
[1] M.M. Clementino, N. Martins-Ferreira, and A. Montoli, On the categorical behaviour of preordered groups, J. Pure Appl. Algebra 223 (2019), 4226-4245.
[2] M. Gran, and A. Michel, Torsion theories and coverings of preordered groups, Algebra Univers. 82, 22 (2021), https://doi.org/10.1007/s00012-021-00709-6.
[3] A. Michel, Torsion theories and coverings of $V$-groups, under review (2021) https://arxiv.org/abs/2104.05616.

Participants sur place (par ordre d’inscription):
Isar Stubbe
William Hautekiet
Pierre-Alain Jacqmin
Aline Michel
John Robert
Joost Vercruysse
Dominique Bourn
Tim Van der Linden
Nicola Carissimi
Marino Gran
Jacques Penon

Participants à distance (par ordre d’inscription):
Andrée Ehresmann
Zurab Janelidze
William Zuluaga Botero
Philippe Gaucher
Michael Wright
Elisabeth Vaugelade
Paolo Saracco
Arnaud Duvieusart
Florence Sterck
Ivo Dell’Ambrogio
Alexis Virelizier
Daniel Tanré
Serge Bouc
Albert Burroni
Julia Ramos González
Sebastian Cea
Jacques Darné
Nadja Egner
Sanjiv Ranchod
René Guitart